 |
|
Measurement Theory of Air Ion |
 |
 |
  1. Measurement principles of air ionsHere are measurement principles of air ions.(1) Ebert's Ion Counter This is the first invented ion counter. 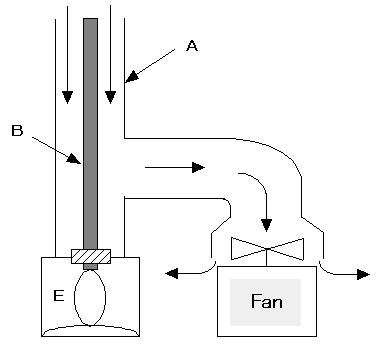
[Fig.1 General idea of Ebert ion counter] A is a cylindrical conductor and it is connected to the ground. B is insulated and coaxial with A. E is a Wolf bipolar electrometer and it is connected to the bottom end of B. The fan on the right bottom part of this image inhales air at the rate of ω/s. When air passes through between A and B, which is charged at V0, B absorbs oppositely charged ions to neutralize itself. When V0 reaches Vt and the value of the capacitance of A-B-E is C, neutralized ions by B is: C(Vt-V0)Air ions are measured in pcs/cc. n, the air ion count, can be given by: n = C(Vt-V0) / eω --- 1The above formula #1 is applicable to air ions with any mobility value. With higher voltages of A-B and lower flow rates, you can measure the total count of small and large ions (n+N). Therefore, N, the large ion count, can be calculated by (n+N) - n. (2) Gerdien Condenser This was developed by applying the principle of the Ebert's Ion Counter. Most ion counters on the market incorporate this technology. The parallel flat plate type ion counter was developed based on this condenser. 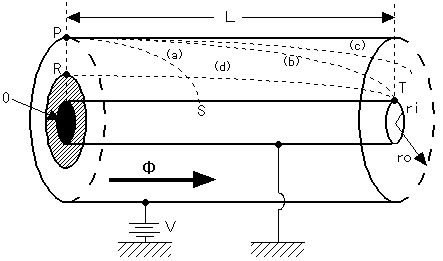
[Fig.2 General idea of Gerdien Condenser] The Fig.2 shows a dual coaxial cylinder. Air flows in the direction of the arrows. ro = ID of outer cylinder ri = Radius of inner cylinder L = Length of cylinder Φ = Flow rate per second V = Voltage applied to outer cylinder Air ions flow into the inner cylinder according to the electronic field in the dual coaxial cylinder. You can measure the number of positive/negative ions when V is positive/negative respectively. If all air ions have the same mobility value and all of those entering from P are captured at S, they are all captured by the inner cylinder. In reality, mobility values of ions are various. kc, the mobility value of the ion captured at T, is defined as the critical point of mobility value, and it is given by: Ions which have higher mobility values than the critical point are all captured. Those which have lower values are not captured and they flow out of the cylinder (C). If ions that reach T (see Fig.2) enter from R (D), ions that pass through P-R flow out, and only those which pass through R-Q (shown with oblique lines) are captured in the inner cylinder. The flow rate ratio of the points of φ (area with oblique lines) and Φ (whole entrance area) is given by: φ/Φ = k/kc(Reference: Misaki, 1960). 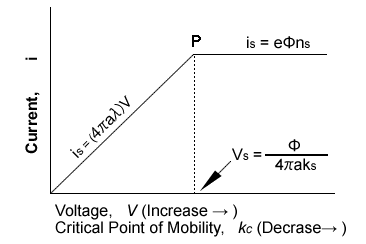
[[Fig.3 Voltage/Current Characteristic Curve of Gerdien Condenser (Misaki, 1976)] To make it simple, let's assume that only small ions exist and the flow rate is fixed. P on the characteristic curveshows that i has reached the saturation point where small ions are all captured and kc, the critical point of mobility value, is equal to ks, the minimum mobility value of the small ions. Vs, the applied voltage, and ns, the small ion density,are given by:
(Reference: Atmospheric Electronic by Shinichiro Kitagawa)
  2. Importance of MobilitySmall air ions have more positive effects on the human body. Large air ions have more capabilities to purify the air.When you study an ionization tendency you need to focus on small or large ions only. This is important when you compare it with ionization tendencies of other locations. Every ion molecule possesses its unique mobility value. It is one of the most important factors to decide on which mobility value (i.e. which ion) to focus on.
  3. Practical measurement of air ions(1) Both ion counts measurement Generally, both positive/negative ion counts change every second in the atmosphere. The ratio of positive and negative ions is a very important factor to understand an ionization tendency. Thus it is ideal to measure both positive/negative ion counts. (2) Simultaneous measurement of both ionsSimultaneous measurement of both ions provides more reliable data.
  4. Significance of Measurement(1) Environmental evaluation A quantitative understanding of ionization tendencies in various locations is one effective way for environmental evaluation. (2) Evaluation of negative ion productsBefore you purchase a negative ion generator (ionizer) it is necessary to know the amount of negative ions it generates. In terms of positive effects on the human body, the amount of small ions detected in the atmosphere is an important factor.

|
 |
||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||

|
|
 |
 |

|
Ion Trading
Universal Plan Co., Ltd.
107 Tachikawa-Lumiere, 3-5-1, Ichiban-cho, Tachikawa-city, Tokyo, 190-0033, Japan
Phone: +81-42-848-5311 Fax: +81-42-848-5148
|
| Copyright (C) Universal Plan Co., Ltd. 1993-2024 Japanese Corporate Number: 1012802002452 (National Tax Agency Japan) |