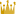ジャック・キューリーおよびピエール・キューリーによるノート(論文) |
 |
 |
   傾いた面をもつ半面像結晶の加圧による分極電気の形成
[ジャック・キューリーおよびピエール・キューリーによるノート(紹介者:フリーデル)1880年]
A. 結晶が一つもしくは幾つかの軸を持ち、その軸端が異なっているものがある。 即ち傾いた面を持つ半面像結晶で、特異な物理的性質を示す。それは温度変化を加えた時に、 上記軸端に、ふたつの反対名の電極が発生すること、即ち熱電気という名前で知られた現象である。 B. 我々は、一連の非電導性物質で、傾いた面を持つ半面像結晶を用いて、分極電気の発生に 関する二つの様式について、比較実験を行った。これらの結晶は、ほとんどが熱電気特性を示す ものである(1)。 [論文名] Développement, par pression, del'électricité polaire dans les cristaux hémièdres à faces inclinées. Note de MM.JACQUES et PIERRE CURIE, présentée par M . Friedel. [掲載誌] Comptes rendus hebdomadaires des séances de l'Académie des sciences,91(1880) 294 [所蔵] The British Library [訳] 科学技術振興事業団  傾いた面を持つ半面像結晶の分極電気について
[ジャック・キューリーおよびピエール・キューリーによるノート(紹介者:デサン)1880年]
A. 前々回の会合で、我々はアカデミーに対して、傾いた面を持つ半面像結晶の分極電気発生の 新しい様式に関する記述を提出した。我々が示した事は、これまでの既知の場合全てで、温度変化 で生ずる効果の向きと、圧力の変化で生ずる向きとの間には、一定の関係があること、この現象を 一般的に言うと、支配している力は何であれ、傾いた面を持つ半面像結晶が収縮する度に、或る向き の電気分極が、膨張する度に、反対向きの電気分極が形成される。 B. 立方晶系――この系に属する傾いた面を持つ半面像結晶は、立方体の4つの3回対称軸という 4つの半面像晶軸を持つ。これらの軸は、同時に電気分極軸でもある。 C. これらの結果を比較してみると、方硼石という例外はあるものの、実験した全ての物質で、 圧縮時の正極は、半面晶像の切子面――これは最も鋭い角度を形成しているもの――を持つ分極 電気軸の先端に現れる事がわかる。方硼石は例外で、反対に、上記事実に対して、興味深い事実を 示している。結局Mallardは、この物質の光学的性質を研究して、 D. 従って、これまでに得られた全ての事実は、一致して以下の事を示している。 取り上げた非電導性で、傾いた面を持つ半面像晶の全ての物質では、半面像晶切子面の位置と、 分極電気の方向とには、同じ関係がある。 [論文名] Sur l'électricité polaire dans les cristaux hémièdres à faces inclinées. Note de MM.JACQUES et PIERRE CURIE, présentée par M . Desains. [掲載誌] Comptes rendus hebdomadaires des séances de l'Académie des sciences,91(1880) 383 [所蔵] The British Library [訳] 科学技術振興事業団  トルマリンを加圧した時の電気の出現則
[ジャック・キューリーおよびピエール・キューリー(1)によるノート(紹介者:フリーデル)1881年]
最初に、トルマリンを加圧した時に現れる電気について、我々の実験から得られた法則について述べ、 続いて、スペースの関係で簡潔に、実験方法と、この法則を実証した時の制約条件について述べる。I.トルマリンの両端面には、向きの違う同量の電気が現れる。法則IVとVを導き出した実験結果を単純に表現すると、“同一の圧力変動に対して、出現する電気量 は、トルマリンの長さによらない”。 [論文名] Lois du dégagement de l'électricité par pression, dans la tourmaline. Note de MM.JACQUES et PIERRE CURIE, présentée par M . Friedel. [掲載誌] Comptes rendus hebdomadaires des séances de l'Académie des sciences,92(1881) 186 [所蔵] The British Library [訳] 科学技術振興事業団  トルマリン及び傾いた面を持つ半面像結晶の電気的現象について
[ジャック・キューリーおよびピエール・キューリーによるノート(紹介者:フリーデル)1881年]
I. トルマリンに関する優れた論文を発表してから、数年後に、ゴーガンは熱電気の現象論を発表 した。彼は、温度変化中のトルマリンを、非常に内部抵抗が大きく、かつ非常に起電力の大きい熱 電堆に模して考える。似たような熱電堆の存在し得る事を示すために、彼は小さなビスマス錐と銅錐 を交互に頂点と頂点、底面と底面を溶接したものを作らせた。 この温度を変えていくと、狭い溶接面は広い溶接面よりも、より速く影響されるので、このシステム は、瞬間的には、一対の熱電堆を構成する事になる。ゴーガンはトルマリンの各分子配列を、これで 模した。実際、よく分かるように、この概念で、彼が打ち立てた定量則を理解できる。しかしながら、 この概念は、受け入れ難い点もあるように思われる。第一に、これでは加圧による電気現象を説明で きない。第二に、電気の出現は、トルマリンのプリズムの側面ではなく、底面だけで見られると言う 事実と一致しない。このことは、以下の実験で、実証できる。 II. 1825年以降、多少とも漠然とながらベクレルやホーブスなどによって提唱されていた分子分極 の仮説によれば、この現象を、ゴーガンの説以上にうまく説明できる。更に以下にトムソンの説を 紹介する:彼の考え方は、かつてのホーブスの説と同じように、分子は、いつも分極しており、 トルマリンの表面に集まっている電気層は、外からみれば中性化している。熱は分極状態に変化を もたらすので、中性状態が崩れる。 III. 我々以前に提議された仮説を検証して、現象の解釈で、我々にとって最も確からしい と思われるものを数式化して、結果を求めた。もっとも、仮定には、疑問点もあるが、それは無視 した。 [論文名] Sur les phénomènes électriques de la tourmaline et des cristaux hémièdres à faces inclinées. Note de MM.JACQUES et PIERRE CURIE, présentée par M . Friedel. [掲載誌] Comptes rendus hebdomadaires des séances de l'Académie des sciences,92(1881) 350 [所蔵] The British Library [訳] 科学技術振興事業団
 |
 |
|||||||||||||||
 |
|||||||||||||||||
|
・マイナスイオン発生器 ・トルマリン原石・パウダー ・入浴用 ・トルマリン素材・シート ・書籍・文献 ・花粉対策 |
・健康トルマリン製品 ・トルマリン化粧品 ・サポーター ・ガードル ・ゲルマニウム特集 |
・ネックレス
・ブレスレット ・お得なセット品 ・マイナスイオン測定器 ・商品一覧 |
| ★ ランキング | ||
|
テレビ・新聞・雑誌・ラジオ等のマスコミで多数ご紹介頂きました。
 |
 |
イオントレーディング
企画・運営 有限会社ユニバーサル企画 (法人番号 1012802002452/インボイス対応済み) 〒190-0033 東京都立川市一番町3-5-1 立川リムエール107 TEL 042-848-5311 / Fax: 042-848-5148 |
|||
|
<< ご注文・お問合せは、電話/FAXでもOK! >>
CopyRight © Universal Plan Co., Ltd. 1993-2024 | マイナスイオンの専門サイト『イオントレーディング』 発生器・測定器は当店で
|
||||